So in the meantime of waiting for a fix, I can’t sit still, so yesterday I ran yet another test whereby I use the correctly calculated G94 mode feedrate for each G1 XA move in my “XA tcB.nc” test case and it proves to also resolve the problem. It worked as expected, just like the G93 solution and photo. This means the solution should be, hopefully, a simple math fix in the LB code that calcs the feedrate in these G1 XA move statement blocks.
Although I doubt they need this, I shared it with LB support yesterday as well, and a reply email indicates there is still some doubt on their part as to the issue being a valid LB bug or not, meaning he mentions speculation that the problem is with my CNC grbl firmware not behaving normal. But everything I’ve read on this linear-angular move topic, including @LightBurn own forum post from Jul '20 that I note at the top of this thread, says otherwise; that my machine is doing exactly what its being coded to do, move a G1 XA coord at the Feedrate interpreted by the linear axis, and synchronize the angular axis feedrate to a speed where both axes meet simultaneously at the XA coord, as specified in distance (mm this case) and degrees. And all the testing I’ve done has borne out the same conclusion, because when the G94 or G93 feedrate is right, the move works perfectly.
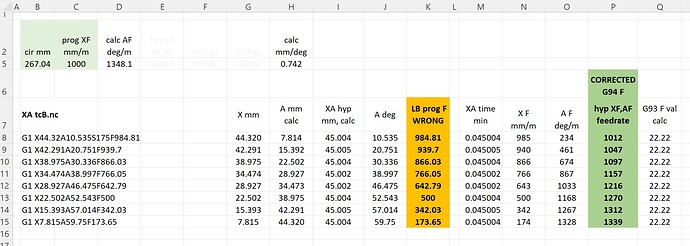
LB is currently using only the calculated X axis feedrate (XF) in mm/m which moves delta X (dX)mm in the time t that it takes to run the hypotenuse of dXmm,dAmm (after calculating dAmm of course, since A is coded in degrees). What’s missing is consideration of the feedrate vector component of the dA axis move distance in degrees. So do the same A axis calc to determine A axis feedrate (AF) using the same dXmm,dAmm time t, leaving the result AF in deg/mm. With these two disparate feedrates, one can now calc the correct G94 feedrate to use on each G1 XA gcode statement, which is the hypotenuse vector of feedrates XF and AF, its ok that they are different units at this point, (in essence they are not different, they are now ‘feedrate’ units for this XA move statement only, and only one feedrate value can be equal for both A and X axes, for this specific XA move statement only). The deg-to-mm, circumference, and desired cutting feedrate considerations have all already been taken into account at this point when time t was calculated as the time (minute units in this case) to cut the hypotenuse (in mm) of this specific dXmm,dAmm at the desired (designed) cutting feedrate.
So the formula for a G94 mode and common XA axes feedrate is: F = sqroot(AF^2 + XF^2), where AF and XF are the feedrates in their respective units/min for each axis to move its respective right angle leg in equal time t to cut the dX,dA hypotenuse line segment at the cutting feedrate in the LB shape layer, 1000mm/min in my test case. This formula also accounts for either AF or XF being zero, which is 0 or 90 deg respectively to the axis of rotation. Of course, repeat/recalc for each G1 XA Line segment or Fill segment or arc chord that is to be coded.
Here is a report comparing the gcode files “XA tcB.nc” which is produced by LB untouched, and “XA tcB G94 corrected.nc”, which I modified only the Feedrate component of each G1 XA line. You can easily see the degree of error in the LB feedrate as the line angle increases 10 degrees in each case from 10 to 80 degrees as shown in the previous post photo with red arrow. The 80 degree line has the greatest degree of over burn and the slowest feedrate, so that stands to reason why its over burnt.
XA tcB G94 corrected feedrate compare.html.txt (9.3 KB)
rotary lin+ang combo feedrate calc V3.xlsx.txt (34.2 KB)